Цуврал нийтлэлийнхээ шинэхэн дугаараар дахин уулзахад таатай байна. Энэ удаад бид SPOJ RGB7 сайтаас сонирхолтой бодлогын тайлбарыг хүргэж, түүнийг хэрхэн оновчтой бодох талаар дэлгэрэнгүй авч үзэх болно.
Шинэ мэдлэг, шинэ сорилтуудыг хамтдаа судалцгаая.
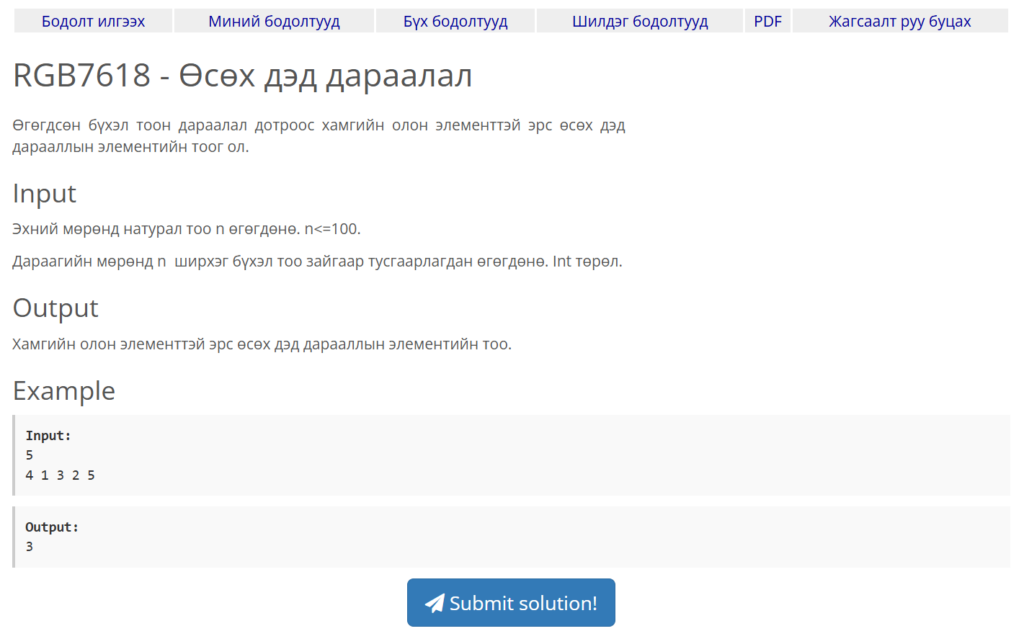
Сонгож авсан бодлого маань RGB7618 – Өсөх дэд дараалал юм. Энэхүү бодлого нь Longest Increasing Subsequence (LIS) буюу хамгийн олон элементтэй эрс өсөх дэд дарааллыг олох тухай юм. Бид өгөгдсөн тоон дарааллаас хамгийн урт өсөх хэсгийг хайж, түүний уртыг хэвлэх ёстой.
LIS гэж юу вэ?
Longest Increasing Subsequence (LIS) гэдэг нь товчоор бол дараалал доторх байрлалыг нь өөрчлөхгүйгээр сонгож болох хамгийн урт өсөх дэд дарааллыг хэлнэ. Өөрөөр хэлбэл, энэ нь дарааллаас сонгож болох дэд дараалал бөгөөд сонгосон элементүүд зүүнээс баруун тийш чиглэлтэйгээр зөвхөн ихсэх ёстой.
Жишээ :
Оролт: 5 2 8 6 3 6
Гаралт: 3
Тайлбар: Дээрх жишээн хувьд боломжит өсөх дэд дарааллууд:
- {2, 3, 6}
- {5, 6, 6}
- {2, 6, 6} ба эдгээрээс хамгийн их урт нь 3 байна.
LIS-г бодох аргууд
LIS-г олох олон арга байдаг бөгөөд тэдгээрээс хамгийн түгээмэл ашиглагддаг хоёр арга нь :
1. Dynamic Programming : (O(n²))
Энэ арга нь Dynamic Programming (DP) буюу бүхэл асуудлыг жижиг дэд асуудлуудад хувааж, тэдгээрийн хариуг хадгалан ашиглах аргыг ашиглан dp[i] массив үүсгэж, тухайн индекс дээрх хамгийн урт өсөх дэд дарааллын уртыг хадгалах юм.
2. Binary Search + DP : (O(n log n))
Энэхүү арга нь Patience Sorting алгоритм дээр суурилдаг бөгөөд LIS-ийг binary search буюу хоёртын хайлтын арга ашиглан хурдан олох боломжтой. Энэ арга нь ихэнх бодлогод илүү хурдан бөгөөд үр дүнтэй байдаг.
RGB7618 бодлогын бодолт
# Оролт авах
n = int(input()) # Элементийн урт
a = list(map(int, input().split())) # Дарааллын элементүүд
# LIS-ийг хадгалах DP массив
dp = [1] * n
# DP ашиглан хамгийн урт өсөх дарааллыг олох
for i in range(n):
for j in range(i):
if a[j] < a[i]: # Өмнөх тоо бага бол
dp[i] = max(dp[i], dp[j] + 1) # LIS уртыг шинэчлэх
# Хамгийн их LIS уртыг хэвлэх
print(max(dp))
Алгоритм:
- dp[i] массивыг үүсгэх → dp[i] нь i-р индекс хүртэлх хамгийн урт өсөх дэд дарааллын уртыг хадгална.
- Анхны утгуудыг оноох → dp[i] = 1 гэж эхэлнэ. Учир нь аливаа нэг тоо өөрөө урт нь 1 дэд дараалал гэж тооцогдоно.
- Давталт ашиглан өсөх дэд дарааллыг хайх:
- i-г 1-ээс n хүртэл гүйлгэж, j-г 0-ээс i-1 хүртэл давталтаар авч, a[j] < a[i] бол dp[i]-г шинэчилнэ.
- max(dp) нь хамгийн урт LIS-ийн утга болно.
Дүгнэлт
| Арга | Цаг | Хэрэглэх нөхцөл |
|---|---|---|
| DP (O(n²)) | O(n²) | n ≤ 10,000 үед тохиромжтой |
| Binary Search + DP (O(n log n)) | O(n log n) | n ≤ 10⁶ үед тохиромжтой |
Хэрэв n (өгөгдлийн хэмжээ) маш том бол Binary Search + DP (O(n log n)) аргыг ашиглах нь илүү үр дүнтэй байдаг. Учир нь энэ арга нь Patience Sorting алгоритм дээр суурилсан бөгөөд Binary Search ашиглан хамгийн тохиромжтой байрлалд элемент нэмэх тул илүү хурдтай ажилладаг. Энэ нь Competitive Programming болон Big Data дээр маш түгээмэл хэрэглэгддэг.
Харин бидний бодож буй бодлогын хувьд n ≤ 100 хэмээн өгөгдсөн тул O(n²) хугацаанд ажиллах Dynamic Programming (DP) арга илүү тохиромжтой юм. DP аргыг ашиглах үед бид давхар давталт (nested loop) ашиглан өмнөх элементүүдтэй харьцуулж, хамгийн их утгыг тооцоолон хадгалах замаар бодлогоо хялбархан бодож чадлаа.



