Программ бичиж байх үед өгөгдлийг ямар нэгэн шалгуураар эрэмбэлэх хэрэгцээ маш их гардаг. Иймээс ч эрэмбэлэх алгоритмууд одоог хүртэл шинэчлэгдэн хөгжсөөр иржээ.
Сонгон эрэмбэлэх арга
- Элемэнтийн олонлогоос хамгийн бага/их элементийг сонгон олно.
- Массивын хамгийн эхний/хамгийн их элементтэй хамгийн бага элементийн байрыг нь солино. Үүний дараа массивын хамгийн бага/хамгийн их элемент нь жинхэнэ эзлэх ѐстой байраа эзэлнэ.
- Үлдсэн (N-1) ширхэг элементийн хувьд (1)- (2) алхмыг давтан гүйцэтгэн өөрийнхөө байх ѐстой байрыг эзлээгүй нэг ч элемент үлдэхгүй болтол нь үргэлжлүүлнэ
c code
#include <stdio.h>
#include <stdlib.h>
int main() {
int a[100], n, i, j, min, temp;
//Massivyn elementiin too
printf(” n = “);
scanf(“%d”, &n);
//Massivyn elementuudiig oruulakh
for(i=0; i<n; i++) {
printf(” a[%d] = “, i);
scanf(“%d”, &a[i]);
}
for(i=0; i<n-1; i++) {
//Khamgiin baga elementiin dugaar buyu indexiig min-d hadgalya
min = i;
for(j=i+1; j<n; j++)
if(a[min] > a[j])
min = j;
//Khamgiin baga elementiig erembelegdeegui khesgiin khamgiin ehnii elementtei bairyg ni solino
temp = a[i];
a[i] = a[min];
a[min] = temp;
}
printf(“Khariu:”);
for(i=0; i<n; i++)
printf(” %d”, a[i]);
system(“pause”);
}
Оруулан эрэмбэлэх арга
Оруулан эрэмблэх алгоритм нь сонгон эрэмблэх алгоритмаас магадгүй илүү уян хатан шинж чанартай. Энэ аргын үндсэн үйлдэл нь эрэмбэлэгдсэн олонлогт эрэмбийг нь алдагдуулахгүйгээр шинэ элемэнт оруулах үйлдлээр тодорхойлогддог. Өөрөөр хэлбэл эрэмбэлэгдсэн элемэнтүүдийн шинэ элемэнтээс их элемэнтүүдийг нэг байрлал баруун тийш шилжүүлэх байдлаар орвол зохих байрлалыг чөлөөлж өгдөг
c code
#include <stdio.h>
#include <stdlib.h>
int main() {
int n, a[100], i, j, temp, k;
printf(” n = “);
scanf(“%d”, &n);
for(i=0; i<n; i++) {
printf(” a[%d] = “, i);
scanf(“%d”, &a[i]);
}
for(i=0; i<n-1; i++)
for(j=i+1; j<n; j++)
if(a[i] > a[j]) {
temp = a[j];
for(k=j; k>i; k–)
a[k] = a[k-1];
a[i] = temp;
}
printf(” Khariu:”);
for(i=0; i<n; i++)
printf(” %d”, a[i]);
system(“pause”);
}
Бөмбөлгөн эрэмбэлэлтийн арга
Элемэнтүүдийг хос хосоор нь сонгон авч буруу байрлалтай бол тэдгээрийн байрыг солино тийм биш бол өөрчлөхгүй хэвээр нь үлдээх гэх мэтээр цааш үргэлжлүүлнэ. Үр дүнд нь хамгийн их утгатай элемэнт массивын төгсгөлд байрлана. Ийнхүү хамгийн их утгатай элемэнт нь өөрийнхөө байрлалыг эзлэх тул түүнээс бусад элемэнтүүдээс тогтох массивын хэсгийг авч түүн дээр өмнөх үйлдлүүдийг давтан гүйцэтгэх процессыг авч үлдэж буй хэсэг дэхь элемэнтийн тоо 2-оос багасахгүй болтол нь үргэлжлүүлнэ
c code
#include <stdio.h>
#include <stdlib.h>
int main() {
float a[100], temp;
int n, i, j;
printf(” n = “);
scanf(“%d”, &n);
for(i=0; i<n; i++) {
printf(” a[%d] = “, i);
scanf(“%f”, &a[i]);
}
for(i=n-1; i>0; i–)
for(j=0; j<i; j++)
if(a[j] > a[j+1]) {
temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
printf(“\nKhariu:”);
for(i=0; i<n; i++)
printf(” %.2f”, a[i]);
system(“pause”);
}
Эдгээр эрэмбэлэх аргууд нь ямар нөхцөлд хэрэглэхээс хамаараад өөр өөр юм шиг боловч .Хамгийн муу тохиолдолд ижилхэн хугацаа зарцуулдаг. Иймээс бидэнд илүү хурдан ажилладаг алгоритм хэрэг болж байна.
Түргэн эрэмбэлэх арга
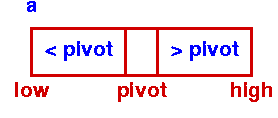
Түргэн эрэмбэлэх техникийн гол элемент нь эрэмбэлж буй өгөгдлийн бүтцийн эргэлт юм.
Пивот нь цуглуулгын төвлөрсөн элемент бөгөөд үүний үндсэн дээр бусад элементүүдийг эрэмбэлэх болно. Пивотыг сонгох хэд хэдэн арга байдаг. Дараах зүйлүүд байна. Эхний элементийг тэнхлэг болгон сонгож байна. Сүүлчийн элементийг пивот болгон сонгож байна. Санамсаргүй элементийг пивот болгон сонгох. Элементүүдийн дундаж утгыг пивот болгон сонгож байна.
c code
#include <stdio.h>
// function to swap elements
void swap(int *a, int *b) {
int t = *a;
*a = *b;
*b = t;
}
// function to find the partition position
int partition(int array[], int low, int high) {
// select the rightmost element as pivot
int pivot = array[high];
// pointer for greater element
int i = (low – 1);
// traverse each element of the array
// compare them with the pivot
for (int j = low; j < high; j++) {
if (array[j] <= pivot) {
// if element smaller than pivot is found
// swap it with the greater element pointed by i
i++;
// swap element at i with element at j
swap(&array[i], &array[j]);
}
}
// swap the pivot element with the greater element at i
swap(&array[i + 1], &array[high]);
// return the partition point
return (i + 1);
}
void quickSort(int array[], int low, int high) {
if (low < high) {
// find the pivot element such that
// elements smaller than pivot are on left of pivot
// elements greater than pivot are on right of pivot
int pi = partition(array, low, high);
// recursive call on the left of pivot
quickSort(array, low, pi – 1);
// recursive call on the right of pivot
quickSort(array, pi + 1, high);
}
}
// function to print array elements
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf(“%d “, array[i]);
}
printf(“\n”);
}
// main function
int main() {
int data[] = {8, 7, 2, 1, 0, 9, 6};
int n = sizeof(data) / sizeof(data[0]);
printf(“Unsorted Array\n”);
printArray(data, n);
// perform quicksort on data
quickSort(data, 0, n – 1);
printf(“Sorted array in ascending order: \n”);
printArray(data, n);
}
Нэгтгэх эрэмбэлэх арга
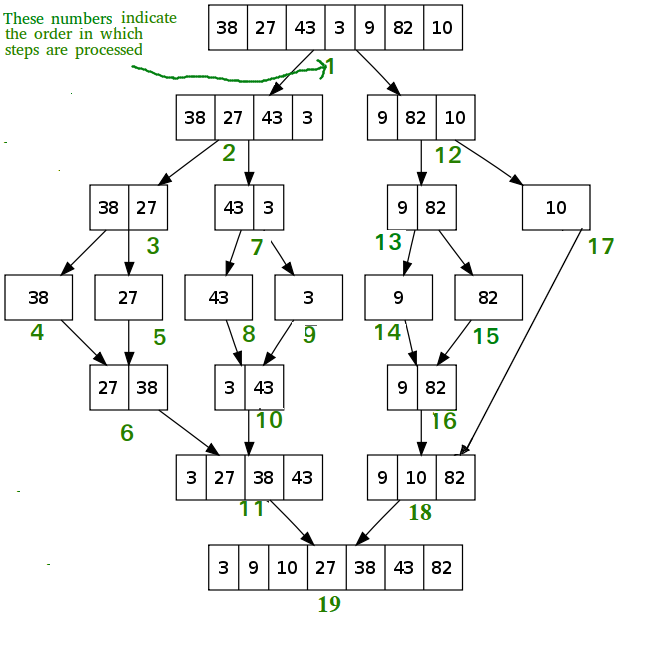
Жагсаалт бүрд нэг нэгж үлдэх хүртэл энэ нь рекурсив функцийн дуудлагыг ашигладаг. Рекурсив функцүүд өөрсдийгөө дууддаг функцүүд юм. Эрэмбэлэгдээгүй жагсаалтыг эхлээд 2 тэнцүү хагаст (боломжтой бол) хуваана. Дараа нь навчны зангилаа бүрд нэг элемент үлдэх хүртэл эдгээр хоёр талыг дахин хагас болгон хуваана. Дараа нь ижил замаар навчнууд хоорондоо нийлдэг, гэхдээ тэдгээрийг зэрэгцүүлэн ялгаж авдаг. Энэхүү арга нь одоогийн байдлаар хамгийн их хэрэглэгддэг ба хамгийн муу тохиолдолд nlog n хугацаанд ажилладаг.
c code
#include <stdio.h>
// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q – p + 1;
int n2 = r – q;
int L[n1], M[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[p + i];
for (int j = 0; j < n2; j++)
M[j] = arr[q + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = p;
// Until we reach either end of either L or M, pick larger among
// elements L and M and place them in the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = M[j];
j++;
}
k++;
}
// When we run out of elements in either L or M,
// pick up the remaining elements and put in A[p..r]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = M[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// m is the point where the array is divided into two subarrays
int m = l + (r – l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// Merge the sorted subarrays
merge(arr, l, m, r);
}
}
// Print the array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf(“%d “, arr[i]);
printf(“\n”);
}
// Driver program
int main() {
int arr[] = {6, 5, 12, 10, 9, 1};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size – 1);
printf(“Sorted array: \n”);
printArray(arr, size);
}
Хайлт
Категори
- 1 минутын уншлага
- 2 минутын уншлага
- AI
- Algorithm
- Bиртуалчлал
- Competitive programming
- computer science
- ide
- webiste
- Аюулгүй Байдал (4)
- боловсрол
- Зөвлөгөө
- Инженерчлэл ба Технологийн Системүүд (2)
- Код
- Компьютерын Шинжлэх Ухаан ба Програмчлал (1)
- Крипто
- Математик
- Өгөгдөл ба Хиймэл Оюун Ухаан (3)
- Программ хангамжийн төсөл
- Систем
- Сурагчдад
- Тархи ба Код
- Технологи, Нийгэм ба Боловсрол (5)
- Технологийн түүх
- Тоглоом хөгжүүлэлт
- Хөндлөнгийн
- Электроник
| M | T | W | T | F | S | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | |



